Effective Accelerationism - Looking into thermodynamic computing
- 1st draft - 08-11-2024
- 2nd draft - 19-11-2024
- 3rd draft - 27-11-2024
Introduction

Looking into Thermodynamic computing
The main idea for Accelerationism comes from Nick Land. One of my all time favourite quotes from him
“Nothing human makes it out of the near-future”
It is both interesting and terrifying. Interesting in the sense that there is a good possibility that evolution of AI will one day catch upto human evolution in terms of IQ(dynamic understanding), cognitive abilities(coffee test by steve wozniak) and therefore, we would no longer have to depend on our deteriorating limbic and cortical systems to make technological progress. Our consciousness can merge at will with AI, climb up the Kardashev scale and live till the end of entropy(maybe something to the likes of Isaac Asimov’s Last question). Our minds will be transferred into a different evolving vessel . But then again, this is all wishful thinking. It is also terrifying if we don’t get out at all and become a mere control point in the feedback loop of capitalism that Nick land mentions. The human element disappears all together.
Since I am a hopeful optimist, I would like to believe in the former. As of now, I am leaning towards a post modernist point of view when I think about acceleration. An information theory/thermodynamic approach.
A lot of progress in our modern day engineering comes from modernist ideas. Think about how first principles works. As you traverse down the binary tree (i.e., pick apart the child nodes), you gain more intuition and then you work your way up to the root node. A lot of our modern day engineering accomplishments come from thinking from first principles theory. As we gain more intuition, we apply engineering skills to make something more efficient. This is a modernist approach.
Even though I am trained as an engineer, my thought process has evolved in the last few years. I got into AI and information theory right out of college and it has definitely had a profound impact on how I approach solving problems. Information theory/ thermodynamic approach suggests that you look at a problem as an isolated system. You observe for gain or loss in entropy by depending on the probability of “states”. The entropy of a system can be defined as the lack of information or uncertainty in the system. This is a post-modernist approach, where uncertainty of a system can be used to gain more information about the internal configuration of a system, rather than breaking it down by first principles. This might just be a point of contention for many and you are free to debate. Very rarely in my 29 years on planet earth, I have had days which has been significant in changing the way I think. Would like to list a few below.
Table of contents
- A few significant days
- A refresher on quantum mechanics and Quantum computing
- Deterministic vs Probabilistic systems
- A Thermodynamic limit
- Entropy and Information theory
- Challenges that we Encounter
- Ways to counter noise
- A Thermodynamic core
- An updated gradient descent
- Dual approximation
- Kardashev scale
- Conclusion
- References
A few significant days
Day 0:-
Back when I was just a lowly undergrad , logic gates were incredibly interesting. Given two inputs you could perform an operation like AND, OR, NOR and you could get a single output “state”. Also, you could try so many different combinatorial logic and get a result. Later on, the applications with counters and flip-flops knew no bounds.
Day 1:-
Compression = Intelligence.
Hutter prize, AIXI had a competition to compress world information . Lossless, not lossy compression was the key to intelligence Hutter prize . Think about the XOR gate mentioned for a moment,
${\displaystyle A\cdot {\overline {B}}+{\overline {A}}\cdot B}$
| A | B | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
XOR gate truth table.
Here, if the inputs A,B is compressed to one OUT, the xor gate waits for input A and also for input B and gives an equivalent output thus helping in compressing the path to a single equivalent path.
For a Xor gate NN, we can use quantization as a compression technique.

XOR-gate weights, source:- Research gate
The error in the XOR problem , varies as a function of a single weight. In larger networks, any single weight has a relatively low contribution to the output. In low dimensional spaces, this can be an issue, but when we consider higher dimensions, the network becomes less likely to get trapped in a global minima and . If the error is low, then the model is likely converge quickly to a non-global minima.
Day 2:-
Attention mechanisms in Transformer models.
When we observe the closeness of words in the context of what we say, there lies an assumed relationship between what was just said and the subsequent word. For instance, when we say the word “eating”, we can automatically assume that “food” is what is supposed to appear in its context. Hence, it is necessary to focus on the “important” weights and how it relates to that particular context [23]. A context vector can therefore be used to estimate how important is the correlation.
Day 3:-
E/acc
In my twitter journey , I found the concept of AI acceleration really fascinating and was thus introduced to the concept of Effective Accelerationism. I will try to explain the philosophy in very simple terms. Let us suppose that all of humanity is in a car and there are two schools of thought. The Accelerationists and the Existentialists [10].
Both the progressives and the accelerationists agree that the trip is good, and that as long as we don’t crash, faster would be better. But:
- The Existentialists think that the car is out of control and that we need a better grip on the steering wheel. We should not accelerate until we can steer better, and maybe we should even slow down in order to avoid crashing.
- The accelerationists thinks we’re already slowing down, and so wants to put significant attention into re-accelerating. Sure, we probably need better steering too, but that’s secondary.
I can elaborate more on the moral standing of the two and the cost benefits and risks, but that is not within the scope of this piece.
The Existentialist school of thought is closer to the probability of doom, p(doom). Meanwhile, the Accelerationist school of thought is aiming to get the optimal probability as soon as possible. p(doom) < p(optimal)
These two schools of thought can be categorized into two questions:-
1) Can AGIs be able to solve the prisoner’s dilemma, the accelerationists seem to think yes, I do too. (More on that later)
2) If not, will the AI agents be able to co-operate or play defect until we are able to Align with the optimal strategy [7].
Let me explain,
Game theory suggests that we have two prisoners, A and B. Now, given a choice they can either choose to confess or choose to defect. The strategy here is that both choose to co-operate - in which case both will get a reduced sentencing or they both choose to defect- in which case they both receive a longer sentencing. If both are trying to choose a dominant winning strategy over the other, both will receive a greater sentencing.
As a proponent for e/acc , I would want both the AI agents to align itself into finding the optimal strategy and thus solve the prisoner’s dilemma. But at the same time, also considering the point of view for the existentialists, anytime there is a higher probability for doom (both defecting), the agents need to radically search for solutions that would lead us to get to the optimal strategy.
My solution initially was to set the exploiter up to maximum and have the agents search the environment , because the other agents are other LLMs…!!. Counterfactual learning or reinforcement learning on the world environment. This will have the search time offset any type of negative growth encountered when we are going through a less than optimal growth phase. Since then muzero has made tremendous strides in dynamic learning.
Day 4:
Particles are just field excitations acting as operators on a 2D Hilbert space.
I would like to have a few more significant days like these.
A refresher on Quantum mechanics and Quantum computing
Let’s think about a quantum mechanical system, and how to measure the state of a Quantum system. We can guess a wave function which is evolving with time, in this case a time dependent schrodinger equation, which is evolving according to some energy operator/ hamiltonian.
$\mathrm{i}\hbar{\frac{d}{dt}}\mid\psi(t)\rangle={\hat{H}}\mid\psi(t)\rangle$
Suppose , we have two energy states, in that case, we can represent the wave function as linear combination of two states. There may not be a definite value for either 0 or 1 at a given point in time, but we can consider a general superposition of the two states, where $\alpha$ and $\beta$ are two complex numbers.
$\mid\psi\rangle = \alpha\mid\psi _{1}\rangle + \beta{\mid\psi _{2}\rangle}$
and the states are:-
$\mid\psi _{1}\rangle and {\mid\psi _{2}\rangle}$
Subsequently for 2 Qubits:
$\mid\psi⟩ = \alpha\mid 00⟩ + \beta\mid 01⟩ + \gamma\mid 10⟩ + …$
where, we basically mean, that if we want to know the probability of the 1st particle , we don’t need to know what the other particles are doing . When we have separable states, measuring one Qbit says nothing about the next Qbit.
Now, let’s think about a classical computer that works on a binary 0 or 1 bits. So, if we wanted to represent N number of bits, ${0, 1} ^ {N}$ will be the word length represented by the processor. Let’s say we want to build a system where we take a string of binary bits 0011 and apply an inverter NOT gate to it, we will get 1100. The word length will be 16 bits.
If we want to build a quantum system to represent N number of quantum bits or Qubits, we have to represent $2^N$ complex numbers. So, if we wanted to simulate the quantum configuration of a system which has N number of bits on a classical system , it presents a frustrating reality in terms of memory , because we have to represent $2^N$ complex numbers. Richard Feynman in the 1980s had addressed this specific problem [22].
But, we shouldn’t be using quantum computers to simulate classical machine learning, it is just inefficient. Quantum computers are great at representing quantum interference patterns, entanglement, superposition but not much for probabilistic algorithms.
Deterministic vs Probabilistic systems
Now, if you think about how NNs work, at its core it is probabilistic and meanwhile classical computers at its core, are deterministic systems. Deterministic systems lacks the randomness, the transistors are either firing a 0 or a 1. This becomes kind of frustrating especially during error correction when a transistor misfires. Another drawback of a deterministic Turing machine is that there is only one possible action. This seems highly inefficient.
The advantage of deep learning is that it can take the randomness of a multi dimensional data and give a concise probabilistic prediction of what the data represents. Whether it be text classification , feature analysis etc [17] . Like encoder decoder models would do by utlizing a latent space(old school VAEs).
There seems to be an energy cost, if we consider deterministic systems especially if there is noise or any adversarial element. GPUs have solved this issue to a certain degree by leveraging matrix multiplication ( the matmul function) , until you are encountering atypical distributions , GPUs won’t be good at sampling those unless you are willing to throw a lot of compute at it. GPUs are pretty good at accelerating matmul , but more complex distributions need a more top down vertical kind of acceleration instead of limiting ourselves to a horizontal left to right sort of acceleration.
Higher Dimensionality reduction still remains a problem. As we will see later, I will outline a way to use sophisticated optimizers to solve just that.
The only thing I can compare it with was when during the early days of RNNs, LSTMs and transformer models, was that of number of parametres was the talk of the town. The focus was solely on building bigger brains. Who could come up with models with more parametres. The parameter count between GPT, GPT-2 and other models were the primary focus. As the years went on , we developed better attention mechanisms with the transformer models, found out ways to perform inference on 70B, 405B parameter models by using different kinds of approximation methods, precision methods, FLOP utilization techniques and the focus shifted from just the number of parametres to performance on benchmarks. It has also helped us to build and understand GPTs on a much more granular level. As I have also learned building BabyGPT
This is the same kind of attention shift that we need from using deterministic systems to probabilistic systems.
Lets understand it with an example:
Sampling issue
Assume, that there are distributions of let’s say 1 dimension. You can sample it in n distributions and store it in memory and now you can have your NNs learn that representation. If you have two dimensions, it takes up n^2 chunks (memory) to sample and for d dimensions , n^d memory is needed. Therefore, the complexity to represent the probability distributions is exponential, if you try to do it on a deterministic system , you will get screwed. This is partly the reason why you had to rely on quantum computers in the first place.
A leap is needed in terms of representing the exponential nature of complexity, and therefore we need a much more evolvable core, which would not only would can produce that sort of compute which is an order of magnitude higher than we what we have today , but also use the energy offset to its advantage. We will get to it down the line.
But first, Let’s talk about a constraint that we need to consider before moving forward.
A Thermodynamic limit
As we train an AI model, its loss slowly drops and then it levels off. If we train a larger model, it will have a lower error rate, but it will require more compute. When we train larger and larger models, we come up with a family of curves. Switching to a log scale, we get a graph, where no model can cross below the dotted line known as Compute Efficient Frontier as evidenced here.
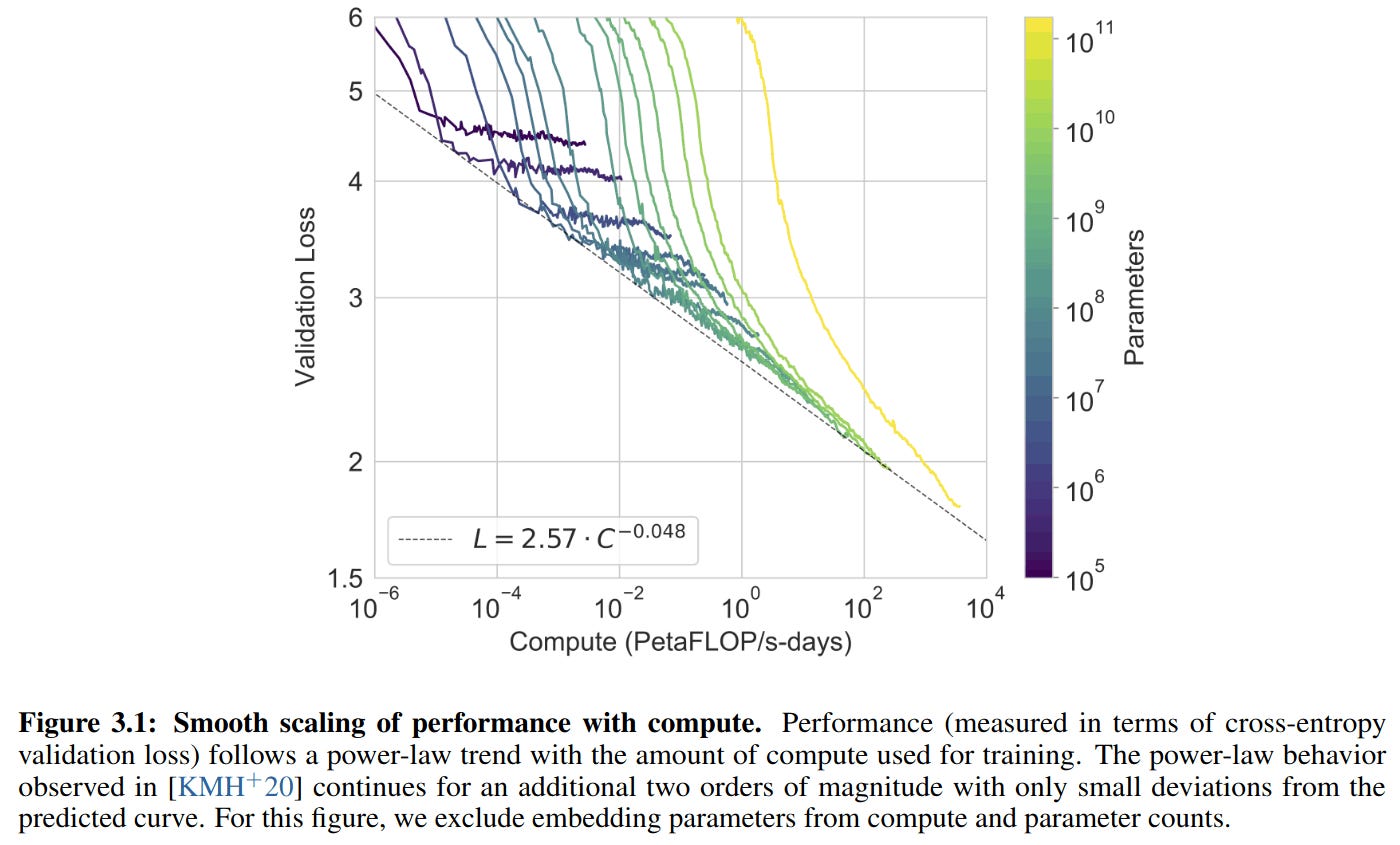
Source:- https://arxiv.org/pdf/2005.14165 - Language models are few shot learners(2020).(GPT-3)
This seems to indicate that there is a fundamental limit in error-rate beyond which no model can surpass, regardless of data or type of architecture.
This has been observed through model-scaling, dataset scaling and compute scaling, as you can see from the power law equations as shown below. The team was quoted in the paper saying:- “We observe no signs of deviation from these trends on the upper end, though performance must flatten out eventually before reaching zero loss”.
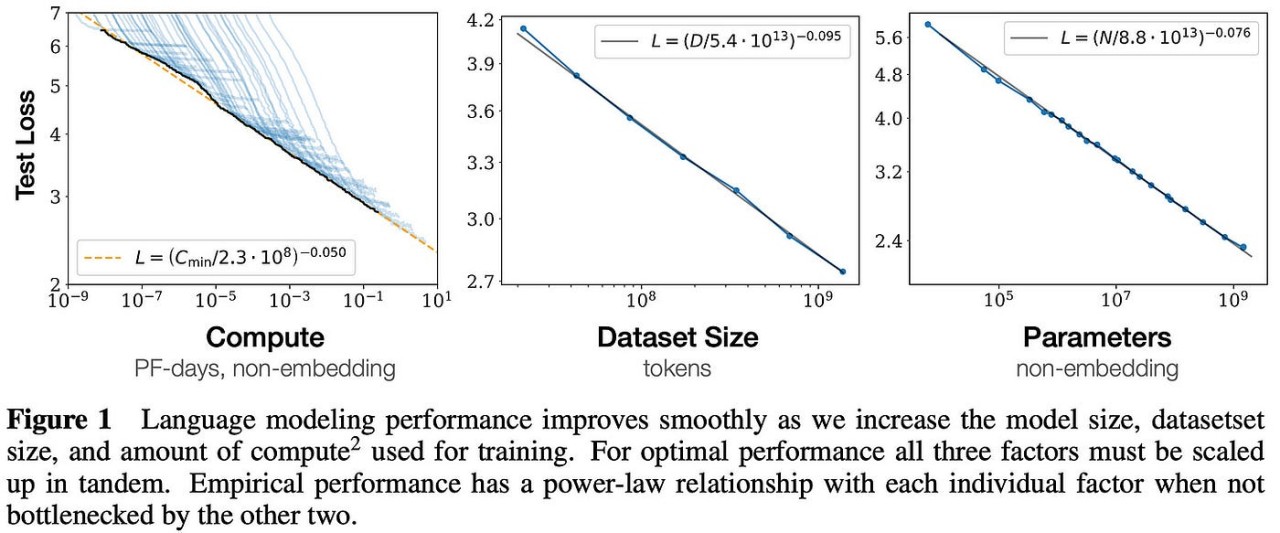
Source:- Neural Scaling laws paper (2020)
The question here is given bigger models, can we get an error rate of zero ?
Plotting the cross -entropy loss vs the L1 loss, we can see that as the model’s probability of correctly predicting the next word in an LLM goes to zero, the cross entropy loss will be very high. Welch lab made a great video about it. Basically, the more confident a model is predicting the correct word in a test set, the closer to zero the average cross entropy becomes.
Scaling Laws for Autoregressive Generative Modeling tried to find out the same using Text-to-Image Loss vs Compute, Video Compute Scaling, language modeling etc.
When we compare GPT-3 vs GPT-4 scale, we get a sort of curvature in GPT-4 vs a straight line in GPT-3.(Its close- when you convert the linear scale below, to a logarithmic scale)

Source:- gpt4 technical report
It has been found since that the scaling laws hold for 13 orders of magnitude. But, we still need to find the best match for the next word in natural language. This uncertainty is called the Entropy of Natural Language. The scaling laws for autoregressive generative modeling paper above, found out just that, by adding a constant error term. But even with the largest language models, the entropy could not be calculated.
The chinchilla paper found out that the cross-entropy loss could get close to 1.69 and level off , but not exactly zero.
The limit
When viewed through the lens of information theory, when we plot cross entropy , we are essentially plotting the missing information.
$H(P,Q)= - \sum_{x} P(x)\log Q(x)$
where, $P(x)$ = true distribution and $Q(x)$ is predicted distribution.
The Entropy $H$ indicates, quantifies the average amount of information (or uncertainty) in a probability distribution $P$.
- Higher entropy means more uncertainty or missing information.
- Lower entropy implies a more predictable system.
Minimizing cross-entropy reduces The K-L divergence , which reduces the missing information.
Similarly, when you plot compute, you’re also plotting energy, which is directly proportional to the information and therefore should produce a straight line. Since all models aren’t equally efficient, there-in lies a thermodynamic limit where increases in compute should increase overall entropy but should decrease with model learning. This is a breakdown of the 2nd law.
So, basically the other side of curvature in the scaling graph represents an impossibilty and an open problem. Considering the fact that the model overfitting could be seen as analogous to a local decrease in entropy. It needs to counterbalance elswewhere, for eg:- when there is poor performance on unseen data.
A generalized second law of entropy could be a remedy to such an issue where local entropy gain/loss from small amounts of statistical fluctuations could be counterbalanced non-locally.
In the next section, we can get a priliminary idea of what I am getting into.
Entropy and Information theory
The connection between entropy and information theory is well known. As mentioned earlier, the entropy of a system can be defined as the lack of information or uncertainty in the system. Assuming all that we know about the internal configuration of a system can be denoted by the probability $P_n$ for the nth state, then Shannon’s entropy [5] would be:
$S = -\sum_{n}^{}P_n \ln P_n$
We can also say that the information in some of the cases of $P_n$ may be zero, so in that case, such a constraint can result in the decrease of entropy.
$ΔI = -ΔS$
where $\Delta I$ can be said as the new information which corresponds to the decrease in entropy, i.e, a decrease in uncertainty in the internal state of the system.
Assume, that an ideal gas is isothermally compressed in a container. It’s entropy will decrease and we will gain information because the molecules are more localized.
An exterior agent can cause a decrease in entropy. Maxwell’s demon is a good example of that. But, information is never free. Therefore while gaining new information , it causes a decrease in entropy of the system, but causes an increase in the overall entropy of the universe.
Now, the question is how does all of this relate to probabilistic systems ?
Let me explain,
As we had talked about an exterior agent can cause certain fluctuations in the amount of entropy, we can use it to offset the amount of energy that a classical computer uses to maintain its determinism. Hence, there will a boost in its efficiency. Considering the fact that a probabilistic system is in thermodynamic equilibrium, the change in uncertainty by the gain in new information can lead to a system being more energy efficient.
Think of Black Holes as probabilistic systems.
Black Holes
Taking a little bit of a de-tour, let’s think of Black holes as objects that are in thermodynamic equilibrium.
So, if any exterior object is thrown into a black hole carrying an entropy S, we can measure the difference in entropy once the object is outside the black hole vs when it is inside. (In a probabilistic system , as evidenced by Shannon’s entropy $ P_n$ - may or may not be known). Therefore, the change in the common entropy ($\Delta S_c$) of a black hole can be measured by
$\Delta S_c = -\Delta S$
and thus the generalized second law as was given by jacob bekenstein. [21]
Similarly in probabilistic systems, uncertainty can be introduced as a measurement of efficiency. If we consider it to be a thermodynamic system, the measurement in statistical fluctutations in common entropy can give us an accurate estimation of training/inference in ML algorithms.
Because, the model weights, including the unused weights will be taken into account. If we can do that, we can close the significant trade-off between compute and memory usage, especially in bigger models.
We may also gain a speedup in training, because the core is evolving along with evolving uncertainty.
What does a thermodynamic core look like ?.
Let’s try to understand from 1st principles.
Challenges that we encounter
Noise
In quantum computing, noise is more often considered to be a hindrance rather than a useful resource. A way in which quantum mechanical systems maintain their states in the face of external factors like thermalization, lossy compression during qubit interaction etc, is called quantum coherence. The loss of such coherence, can lead to noise becoming a hindrance to an algorithm rather than a resource. This is also partly a reason why quantum computers haven’t really become commercially viable. A loss in coherence can lead to otherwise efficient algorithms (with polynomial scaling) into inefficient algorithms (with exponential scaling). This essentially destroys whatever quantum speedup that one would hope for over classical methods.[2] [9]
Interference with heat and entropy dynamics
Thermodynamic systems are sensitive to heat. Heat, in this case may cause the same problems in a thermodynamic computer just as we have in a quantum computer, therefore it needs to be well shielded. Refrigeration is also needed to maintain common entropy along with the local entropy of the system.[2]
In AI, generative modeling or Bayesian inference require complicated entropy dynamics. In generative modeling, a gaussian distribution is typically of higher entropy and we need to gradually move towards a structured prediction. Similarly, in Bayesian inference, the weights of the model must be transformed from a high uncertainty situation (the prior distribution) to a low uncertainty situation (the posterior distribution) as information about the data is introduced during training.
Ways to counter noise
As mentioned above that loss in coherence can lead to inefficient algorithms, there are ways to counter it as well.

The blue line leverages quantum tunneling to find global minimum., source:- wiki
Thermal fluctuations in isolated systems can result in the system exploring different minima in the landscape before settling down in a high-quality minimum.
A Thermodynamic core
In one of the previous sections , we had talked about how to design a thermodynamic core using first principles.
Early classical computers followed the Von-neumann architecture. Then as time went on, we evolved to a single bus system, thus “streamlining” the architecture using MCUs. These processors are scalar in nature. Later on, we evolved to graphic processors which are very good at leveraging matrix multiplication orders of magnitude greater than CPUs. The streaming multiprocessors (SMs) of GPUs are effectively vector processors, and can process thousands of operations on a single clock cycle.
A thermodynamic core has to follow stochastic processes, because we are taking advantage of a d- dimensional Eucledian space and therefore utilizing uncertainty. The randomness in a system can generate many outcomes and thus, it will be easier to sample. Classifications become simpler if we use stochastic processes- the state space is easier to sample.
We need to design a processor which will be able to solve Markov processes , and therefore relax a noisy harmonic oscillator, in the presence of thermal fluctuations. This is one way of doing it.
An Updated Gradient Descent
One of the main issues facing Neural networks is destructive interference. The addition of new training data leads to the forgetting of what was already learned. We need a new type of gradient descent which would represent the underlying geometry of a parametre space and is adjusted dimensionally(i.e, rescaling prior distribution) by utilizing the Fisher information matrix , which is exactly what we were looking for when it is time to represent/learn atypical gaussian distributions [15].
We can use it to represent a curvature of information on a riemannian manifold, and thus reduce the dimensionality issue and also provide an efficent optimizer to solve for computational overhead.
A few points here,
-
Think about a normal gaussian distribution in d dimensions. In order to sample, we have to apply a squishing function which is the covariance matrix of the score and also make sure that prior learning remains intact.
-
We need to make the output of a network after applying the gradient function closer to that of the original network. For that, the gradient needs to move in a direction to preserve prior learning.
-
We also need to make sure that the dimensionality problem gets fixed.
A way to do it is to estimate a cost function, followed by optimizing its loss function, then measure how different two models are using K-L divergence between the conditional probability distributions that they represent [15].
Let’s understand how to design one.
We will divide it into three steps:-
- Cost function and optimizing loss function
- Optimize cost function to parametre space and update.
- Applying K-L divergence to observe change between conditional probability distribution and update.
Table of Notations
| Notation | Description |
|---|---|
| $h$ | Objective function |
| $θ$ | Network parametres |
| $S$ | training set |
| $w$ | weight gradient |
| $x, y$ | input, pairs |
| $L$ | Loss function |
| $f$ | Prediction function |
| $F$ | Fisher information matrix |
| $ϵ$ | Learning rate |
| $ϵ_k$ | step size parametre at iteration k |
| $P_{x, y}$ | learned distribution $P_{x, y} (\theta)$ |
Step 1:-
The goal of optimization is to find some setting for two paramteres $\theta$ , so that for each input $x$ , the output of the network matches closely with the given target output with some loss [3]. So, let’s consider a cost function $h(\theta)$
So,
$h(\theta) = \frac{1}{\mid S \mid}\sum_{(x,y)\in S } L(y, f(x, \theta))$
where, $f(x, \theta)$ is the prediction function measuring the disagreement and $L$ is the loss function.
Now, the next step is to optimize the loss function.
A couple of things to keep in mind, while we are optimizing the loss function, where $\epsilon$ is the learning rate.
- If the learning schedule is small, then the covergence to minimum is also slow [6].
- If it is high, then the algorithm may be unstable,(i.e., oscillating) or even overshooting . There is a possibility, that it may diverge. If the rate is within $\epsilon_k = \epsilon > 0$, then we can say that there is good divergence.
The goal here was to move the gradient in a direction that keeps the prior learning intact. So, the direction of motion of $d_k$ has to be in the opposite direction. Therefore, it must project towards the negative gradient , $- \nabla f(x)$. This is called steepest gradient descent that moves in the opposite direction [6].
So, the algorithm can be devised as :
Algo 1 (steepest descent):-
$x ∈ R^{n}$
$k =0, 1, 2…$
$x_{k+1} \longleftarrow x_k - \epsilon_k\nabla f(x_k)$
Algo 2 (Gradient Descent)
for $k =0, 1, 2…$
$x_{k+1} \longleftarrow x_k + \epsilon_kd_k$
where $R$, is the Riemannian manifold over the space of distributions
So, the negative gradient function for the steepest descent can be considered as the instantaneous rate of reduction in $h$ per unit change in $\theta$ [3] .
Therefore,
the function at a point $x$ in the direction of $d$ can be written as,
$\nabla_{d} f(x) = \lim_{\epsilon \to 0} \frac{f(x + \epsilon d) - f(x)}{\epsilon}$
So, at each step size k, the function will be:-
$\lim_{\epsilon \to 0} f(x_k + \epsilon d_k)$
And the optimal rate will be:
$\epsilon_{k} = argmin_{\epsilon_{\ge 0}}f(x_k + \epsilon d_k)$
But, this is a little bit costly, hence the Armijo rule to reduce complexity [6].
Step 2
The second step is to optimize $h$ with respect to negative gradient $-\nabla h$ , and thus represent it on a geomteric paramtere space. It will look something like this [3],
$\frac{-\nabla h}{\mid\mid \nabla h \mid\mid} = \lim_{\epsilon \gets 0} \frac{1}{e} e_k$
Or,
$\frac{-\nabla h}{\mid\mid\nabla h \mid\mid} = \lim_{\epsilon \gets 0} \frac{1}{\epsilon}argmin _{d:\mid\mid d \mid\mid ≤0} h(\theta + d)$
where,
$d$ is the gradient direction.
$\left| \left| \right| \right|$ –> because we are considering the gradient on Eucledian space.
Now, we need to adjust the gradient descent by accounting for the underlying geometry of the parameter space, as represented by the Fisher Information Matrix.
This adjusted gradient descent is known as the Natural gradient Descent. So, weight gradient in a NN by inverse Fisher info, is represented by eqn (1):-
$w_{t+1} = w_t - ηF(w_t)^{-1} \nabla f_i(w_t)$
for a mini batch $i$ where,
- $F(w_t)^{-1} \nabla f_i(w_t)$ is the natural gradient
and,
-
$\nabla f_i(w_t)$ is the gradient log likelihood w.r.t $\theta$
-
$\eta$ is the learning rate.
Step 3:-
We can apply K-L divergence over the learned distribution $P_{x, y} (\theta)$ to see how much the changing of the weights , changes the output of the neural net.
Therefore,
$KL(P(y; \theta) \mid\mid P(y ; \theta + d)) \sim \frac{1}{2} d^{T} F d$
This represents the changes in the gradient direction to 1 , because we are moving down the gradient , but changing the output of the weights as little as possible.
$d$ is a dimensional weight vector which is a $d * d$ matrix. Therefore, it can be used to fix huge dimensions(millions..!!) as was our goal.
The Natural gradient descent can be defined as:-
$\nabla ^ {‘}.h = F^{-1} \nabla h(\theta)$
Therefore, for a Natural gradient descent optimizer from eq (1) will be:
$\theta_{t+1} = \theta_t - \eta F^{-1} \nabla h(\theta_t)$ [13]
and this is the Update rule.
Where F will be,
$F = -E_{P_{(x,y)}}[H\ log_{P_{(x,y)\mid\theta)}}]$
It is still a bit computationally expensive to implement NGD, but it provides us with a path to harness uncertainty in a gaussian distribution and reduce high dimensionality ( n^d). Solving the computational cost at every epoch needs to be the goal and thus we consider more sophisticated optimizers, which can easily coverge in highly oscillating systems.
Beyond softmax
The role of softmax in DL is to convert a vector of logits into probability distributions. Softmax allows for the temperature parametre $\theta$ to adjust the probability.
One limitation of the softmax function is that whenever there is an out-of-distribution input, it can mess up the probability. A higher logit can disrupt the probability distribution and thus hinder the sharpness of decisions made by a NN during inference time. This issue becomes more pronounced as the problem size increases with time.
This paper provides an approach where the authors attempt to adjust the temperature parametre to control the entropy of input coefficients. Adaptive temperature increases the sharpness of decisions made by the NN.
A theoretical limitation of softmax is that sharpness diminishes as more items are added.
One way to remedy such an issue would be to use the logits of the “prior distribution”. We can come up with stochastic methods to sample those use $argmax$ to branch out $n$ -samples. When dimensionality of said samples are high, a variance in entropy can be calculated to repurpose unused logits that were causing problems for larger distributions. This Github repo seems closest to that analysis.
I will see if I can work out the math for it.
Dual approximation
We can extend this thought process to a probabilistic system/ model where the prior distribution not only remains intact, but there is a way to minimize the upper limit to the divergence. In the previous example, we were capping off the learning rate between $\epsilon_k = \epsilon > 0$ so as to prevent too much divergence.
In the following example, we can approximate an upper limit with respect to some input information, then the action can be characterized w.r.t the output. Therefore, a dual optimization can be aprroximated from active inference. This upper limit is called free energy.
So, free energy can be used to characterize input perception to output action. Hence, there can be systems which can optimize this way as well.
i/p perception ⟶ free energy minimization ⟶ o/p action.
Once again, we have to estimate the weight change. Now, it is between prior probability distribution (i.e before the training data) and posterior probability distribution (i. e after the action).
The flowchart for a model may look like:-
Perception ⟶ Internal states ⟶ Action ⟶ External hidden states ⟶ perception

Free energy system for a generative model, source:- dialectic systems
- Perception:- Some input distribution
- Internal states:- internal hidden state , before getting perceived by an agent. $\mu$
- Action state:- Possible Actions that can be made by the agent. $a$ and $s$
- Hidden state:- external hidden state (not being directly accessible). $\psi$
Now, if we consider the states indiviually, for a generative model.
-
External states and actions = $p_{ext}(s\mid \psi ,a, (\theta + d))$, where $s$ is the active state perceived by the agent. $d$ is the gradient direction.
-
Action state = $p_{A}(a\mid \mu ,s, \theta)$ Agent’s actions depend upon its internal states.
- Hidden state = $p_{int}(\mu \mid s, \theta)$ (internal state).
- Model environment - Stochastic model of env $p_{\Psi}({\dot {\psi }\mid \psi , a, \theta)}$
and $\theta$ is the network parameter
Therefore, the joint probability would be:-
$p_{bayes}(\dot \psi ,s, a, \mu, \theta\mid\psi) = p_{int}(\mu \mid s, \theta)p_{\Psi}({\dot {\psi }\mid \psi , a, \theta)}p_{A}(a\mid \mu ,s, \theta)p_{ext}(s\mid \psi ,a, (\theta + d))$
[Note:- By adding $d$, we are essentially considering an ordered distribution - a slight deviation from the example given on wiki]
“Bayes rule” will determine “posterior probability”. We can apply KL divergence to see the change between $q$ which is an approximation to $p_{bayes}$ and $p_{bayes}$
Now, since the objective function $KL(Q_{x,y} \mid\mid P_{x,y}(θ)) = \int q(x, y) log \frac{ q(x, y)}{p(x, y \mid \theta)}dxdy$
is equivalent to ,
$E_{Q_x} = KL(Q_{y \mid x} \mid\mid P_{y \mid x}(θ))$ [3]
So, free energy can be simplified into,
$F(\mu, a, s, \theta) = E_{Q _(\dot\Psi)}$
$*p_{bayes}(\dot \psi ,s, a, \mu, \theta\mid\psi)$ - H(entropy)
which is equal to,
$= -\log p_{ext} + KL(q(\dot\Psi \mid, \mu, a, s, \psi, \theta)] \mid\mid p_{bayes})$
where $H(entropy)$ is the missing information.
So,
$F(\mu, a, s, \theta) \ge -\log p_{ext}$
where, $\log p_{ext}$ is the surprise element. The surprise element is the self minimization.
Free energy minimization techniques can be considered to be in direct correlation with counterfactual world modeling. A Counterfactual World Model, let’s say $\psi$ ,
takes an input and constructs an internal representation of the scene. Just like we have internal hidden states in the generative model example above, this representation can be used to generate counterfactual simulations of what would happen if different events occured. It can be used to estimate the changes within the stochastic environment and compute the actions and external states. Predictions can also be made about the dynamical properties of the system. Here is a paper that touches upon it somewhat.
Kardashev scale

Kardashev scale, source:- dialectic systems
A log scale that determines the how far a civilization can progress depending on its energy usage.
Carl Sagan defined intermediate values (not considered in Kardashev’s original scale) by interpolating and extrapolating the values given for types I (1016 W), II (1026 W) and III (1036 W), which would produce the formula
$K=(log P-6)/10$
where K is a civilization’s Kardashev rating and P is the power it consumes, in watts. Using this extrapolation, an early Type 0 civilization, not defined by Kardashev, would consume about 1 MW (106 W) of power.
Type I
A civilization that can harness all the energy that its home planet receives. (like Earth)
Type II
A civilization that can harness all the energy of its nearest star and
Type III
A civilization that can harness all the energy from its galaxy.
Technological progress needs to advance to a point where we can be a type 3 civilization. The second law of thermodynamics states that the entropy of systems cannot decrease with time and must always arrive at a state of thermodynamic equilibrium. Simply put, the total amount of entropy (disorder or chaos) always increases.
The Kardashev Scale looks at only energy usage but this raises the concern that any civilization that lets its energy grow out of control may commit suicide.
Since the total disorder of the universe is going to continue to soar, an “entropy conservation” civilization needs to invest effectively in heat management and resourse management [25].
An “entropy wasteful” civilization continues to expand its energy consumption without limit. Eventually, when the home planet becomes uninhabitable, the civilization might try to flee its excesses by expanding to other planets. But, if the entropy grows faster than the civilization’s ability to escape , it will destroy itself.
Conclusion
We started off by postulating the difference between a modernist(first principle’s approach) vs a post-modernist approach, which is information theory. The best of both worlds are currently in use as we saw recently with Elon Musk’s and SpaceX’s milestone accomplishment, when they caught the booster in the 1st attempt. When we use the post modernist approach we get thermodynamic computing/probabilistic computing. Extropic and Normal Computing are two great pioneers in the field right now.
We move on towards e/acc and talk extensively about game theory. A lot of AI doomers believe that Prisoner’s dilemma cannot be solved, because every one is aiming for a dominant winning strategy, but it can be optimized. E/acc in parts, should be , in my opinion steering towards the optimal winning strategy and that is what makes it slightly different than accelerationism.
We continue our journey into the more technical side of e/acc. Starting from QM and the need for a probabilistic system over deterministic systems. We discusss some of its challenges as well. A new optimizer is introduced which will help us to work with higher dimensions and also free energy systems has been touched upon, which provides deeper intuition about a dual approximation techniques in generative modeling.
As I had mentioned in the beginning about ascending up the Kardashev scale, a post-modernist way of thinking can help our civilization to achieve just that. As far as e/acc is concerned, it is just one of many such philosophies. I haven’t gone deep into acceleration, yet. There’s a lot to cover with Land, deleuze, post-humanism, techno optimism etc. It is still in the cards, and one day there may be a post.
Since, I am keen on e/acc and thermodynamic computing , this has been a sort of introduction on how I would like to contribute to e/acc going forward. I would like leave you with this
“Not to withdraw from the process, but to go further, to ‘accelerate the process’, as Nietzsche put it: in this matter, the truth is that we haven’t seen anything yet.” – Deleuze and Guattari, Anti-Oedipus
References:
-
https://www.statlect.com/glossary/information-matrix
- https://arxiv.org/pdf/2302.06584 - Thermodynamic AI and fluctuation frontier
- https://arxiv.org/pdf/1412.1193 - New Insights and Perspectives on the Natural Gradient Method
- https://news.ycombinator.com/item?id=40466826 - Thermodynamic natural gradient descent
-
https://arxiv.org/pdf/1604.07450 - Quantum information chapter 10- Shannon entropy
-
https://katselis.web.engr.illinois.edu/ECE586/Lecture3.pdf - Steepest gradient descent algorithm
-
https://geohot.github.io/blog/jekyll/update/2023/08/16/p-doom.html - p(doom)
-
https://cba.mit.edu/docs/papers/96.isj.ent.pdf - Signal entropy and thermodynamics of computation
-
https://arxiv.org/pdf/2303.09491- Challenges and Opportunities in Quantum Machine Learning
-
https://forum.effectivealtruism.org/posts/hkKJF5qkJABRhGEgF/help-me-find-the-crux-between-ea-xr-and-progress-studies - Effective altruism
- https://notesonai.com/kl+divergence - KL divergence
- https://arxiv.org/pdf/2308.05660 - Thermodynamic linear algebra
- https://arxiv.org/pdf/2405.13817 - Thermodynamic Natural Gradient descent
- https://www.youtube.com/watch?v=pneluWj-U-o - Fisher Information
- https://www.youtube.com/watch?v=QmM6_qBHuvM&t=5s - CIS 522 Natural gradients
- https://www.youtube.com/watch?v=VqXnhcpiXZw&pp=ygUXdGhlcm1vZHluYW1pYyBjb21wdXRpbmc%3D - Thermodynamic computing explained in 5 minutes
- https://www.youtube.com/watch?v=OwDWOtFNsKQ&t=1898s&pp=ygUXdGhlcm1vZHluYW1pYyBjb21wdXRpbmc%3D - Thermodynamic computing extropic
-
https://www.normalcomputing.com/blog-posts/thermox-the-first-thermodynamic-computing-simulator#heading-7 - thermox: The First Thermodynamic Computing Simulator
- https://www.normalcomputing.com/blog-posts/a-first-demonstration-of-thermodynamic-matrix-inversion-3#heading-3 - Matrix inversion
- https://www.normalcomputing.com/ - Normal computing
-
https://journals.aps.org/prd/abstract/10.1103/PhysRevD.7.2333 - Bekenstein Hawking entropy.
-
https://arxiv.org/pdf/2106.10522#:~:text=In%20May%201981%2C%20Feynman%20spoke,using%20conventional%20classical%20digital%20computers. - Feynmann quantum computing
- https://lilianweng.github.io/posts/2018-06-24-attention/ - Attention Mechanism by Lilian weng.
-
https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence- KL divergence wiki.
-
https://kardashev.fandom.com/wiki//Entropy#:~:text=The%20Kardashev%20Scale%20looks%20at,must%20be%20taken%20into%20account.
-
https://en.wikipedia.org/wiki/Free_energy_principle#Free_energy_minimisation_and_thermodynamics - Free energy principle.
- https://arxiv.org/pdf/2410.01104 - softmax is not enough
** Diagrams could not be included in the pdf **